Exercise 3-78(2)
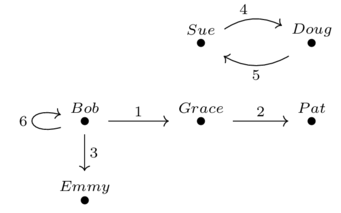
Draw the instance \(I\) in Example 3.77 as a graph.NOCARD
Solution(1)
Consider the schema \(\mathfrak{g} := \boxed{\overset{Email}\bullet \overset{sentBy}{\underset{receivedBy}{\rightrightarrows}} \overset{Address}\bullet}\)
And an example instance: \(\mathfrak{g}\xrightarrow{I}\mathbf{Set}\)
| SentBy | ReceivedBy | |
|---|---|---|
| 1 | Bob | Grace |
| 2 | Grace | Pat |
| 3 | Bob | Emmy |
| 4 | Sue | Doug |
| 5 | Doug | Sue |
| 6 | Bob | Bob |
Data migration functors \(\Sigma_!,\Pi_!\) go from \(\mathcal{C}\) Inst to 1-Inst, but we showed that 1-Inst is equivalent to Set in Example 3.53.
\(\Sigma_!\) tells us the mailing groups, the "connected components" in \(I\):
| 1 |
|---|
| Bob-Grace-Pat-Emmy |
| Sue-Doug |
\(\Pi_!\) tells us the emails that were sent from a person to themselves
| 1 |
|---|
| \(Em_6\) (Bob) |
For any category \(\mathcal{C}\) there is exactly one functor to the category 1, let’s call it \(!\) Where does it send each object and each morphism?
There is only one object to send each object to and only one morphism to send each morphism to. Because everything in the target is equal to everything else, all functor constraints are trivially satisfied.
Draw the instance \(I\) in Example 3.77 as a graph.NOCARD
